Embedding

Quickstart

:{
do
  let yourMSF = count
  ls <- embed yourMSF ["input0", "input1", "input2"]
  print ls
:}

:{
do
  let yourSF = integral
      dt = 1 / 60
  ls <- runReaderT (embed yourSF $ replicate 10 123.0) dt
  print ls
:}

:{
do
  let yourSF = integral
      dt = 1 / 60
  ls <- embed (runReaderS_ yourSF dt) $ replicate 10 123.0
  print ls
:}

Basics

Read the [YamCade03] and [FrpRefac16] papers and if you don’t understand it lets do it step-by-step. If you need a more verbose version of these papers there is [FrpExt17].

A MSF describes a general stepper function which moves a simulation forward in a causal manner. In it’s most basic for it’s just “step step step…”, but we can apply Monads to describe more complex forms of what this step is (like time).

In a real program we are going to run MSFs in an endless loop called reactimate. With embed we can create deterministic simulations with predefined inputs and them once. This is great for learning and debugging and lets us increase the difficulty gradually.

Here is how you can find out how embed is defined:

1. Search with Hoogle.

2. Look up the definition on Hackage.

3. Hover over the function name in Visual Studio Code.

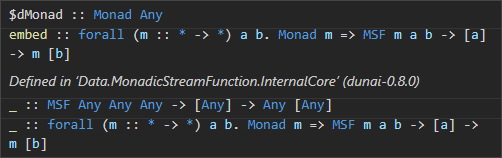
4. Start GHCi and ask for the type:

>>> cabal repl
>>> :t Data.MonadicStreamFunction.embed
-- embed :: Monad m => MSF m a b -> [a] -> m [b]

Let’s use GHCi to start a simple embed example:

>>> cabal repl
>>> :m Data.MonadicStreamFunction
>>> embed (arr (+1)) [1, 2, 3]
-- [2,3,4]

It is important to note that GHCi always provides an IO Monad if necessary, which means the free type variable m is inferred as IO. I think it’s a bit confusing however to see what’s going on when, sometimes a Monad is provided by GHCi, and sometimes it’s not required, but in the end we will write full programs which all run within a main :: IO (). Thus I’m going to avoid the GHC interpreter for now and we load examples directly.

Open a text editor and write the following text into a file named main.hs:

{-# LANGUAGE Arrows #-}

import Data.MonadicStreamFunction

main :: IO ()
main = do
  putStrLn "Hello world"

To start the program:

>>> cabal repl helloworld
>>> main
-- Hello world

In main replace the code with:

main = do
  [1,2,3]
-- > ERROR! Couldn't match expected type: IO t0 with actual type: [a0]

This doesn’t work because main needs to return a Monad. Thus we write:

main = do
  pure [1, 2, 3] -- or: return [1, 2, 3]
-- > [1,2,3]

Note

Recall that pure = return (somtimes called unit) but we are going to use pure all over this text to avoid confusion with keywords used in imperative languages. return in Haskell is an ordinary function and not any special language construct.

embed needs a MSF as parameter, we can always use an identity Arrow which only passes through values. This is not very exciting but helps us understand how everything is build up.

main = do
  embed (arr id) [1, 2, 3] -- or: embed returnA [1, 2, 3]
-- > [1,2,3]

With arr we can add pure functions into an Arrow network.

main = do
  embed (arr (\n -> 1 + n)) [1, 2, 3]
-- > [2,3,4]

-- embed (arr (1 + )) [1, 2, 3] -- suggested by Haskell Language Server

Note that embed returns a Monad similar to pure. We could also bind it to a variable and print it:

main = do
  ls <- embed (arr (1 +)) [1, 2, 3]
  print ls
-- > [2,3,4]

-- print =<< embed (arr (1 +)) [1, 2, 3]

So far you might be wondering: What’s the point? If all we want is a converted list, why don’t we just use fmap?

We are going to use the recursive arrow count now to build up a state.

count :: (Num n, Monad m) => MSF m a n

main = do
  embed count ["foo", "bar", "baz"]
-- > [1,2,3]

count doesn’t care what it gets. The type variable a is free. The function only counts how often the simulation was called. So it’s okay to just use unit types or any other type:

main = do
  embed count [(), (), ()]
-- > [1,2,3]

Internally count uses the function sumFrom, which again uses the fundamental function feedback.

feedback :: Monad m => c -> MSF m (a, c) (b, c) -> MSF m a b

Note

It’s interesting to see how some of these functions are implemented in source.

-- | Sums the inputs, starting from an initial vector.
sumFrom :: (VectorSpace v s, Monad m) => v -> MSF m v v
sumFrom = accumulateWith (^+^)

-- | Applies a function to the input and an accumulator,
-- outputting the updated accumulator.
-- Equal to @\f s0 -> feedback s0 $ arr (uncurry f >>> dup)@.
accumulateWith :: Monad m => (a -> s -> s) -> s -> MSF m a s
accumulateWith f s0 = feedback s0 $ arr g
  where
    g (a, s) = let s' = f a s in (s', s')

-- | Well-formed looped connection of an output component as a future input.
feedback :: Monad m => c -> MSF m (a, c) (b, c) -> MSF m a b
feedback c sf = MSF $ \a -> do
  ((b', c'), sf') <- unMSF sf (a, c)
  return (b', feedback c' sf')

Todo

Add discussion for feedback function

Reader

Warning

There is an error in refactored 3.2 lifting. There is no liftS :: (a -> m b) -> MSF m a b function. Searching Hoogle for (a -> m b) -> MSF m a b we get arrM. liftS should be introduced as an deprecated alias for arrM.

{-# DEPRECATED liftS "Use arrM - the alias liftS was only used in the refactored paper." #-} liftS = arrM

already mentioned here

Recall that the Reader monad is a readonly context which in our case could be used to inject config files. We are using a very simple config here which just says “how much should be added by each count”. The runXyz functions of most Monads are used to peel of the monadic context and reveal the value within the Monad, which is usually used at the outermost calling site.

Todo

what’s the point? why not just pass the config as a value?

runReader :: Reader r a -> r -> a

Note how r is gone in the final result.

countReader :: MSF (Reader Int) () Int
countReader = count >>> arrM (\x -> ask >>= (\e -> pure (x * e)))

main = do
  runReader (embed countReader [(), (), ()]) 5
-- > ERROR: Couldn't match expected type: IO t0 with actual type: [Int]

Note that a MSF is also a Monad defined by the m type variable and thus countReader is a Reader Monad. If we use runReader here, we peel of the Reader Monad, we get what’s inside, a plain value. Either we bind the variable (with >>=) or just assign and print it.

main = do
  let ls = runReader (embed countReader [(), (), ()]) 5
  print ls

--print $ runReader (embed countReader [(), (), ()]) 5

Refinement

Let’s shorten the definition of countReader a bit. Recall that <$> is just an alias for fmap which is function application within a context (in this case, the Reader Monad).

 ($)  ::                    (a ->   b) ->   a ->   b -- application operator
(<$>) :: Functor     f =>   (a ->   b) -> f a -> f b -- applying a function within a context
(<*>) :: Applicative m => m (a ->   b) -> m a -> m b
(=<<) :: Monad       m =>   (a -> m b) -> m a -> m b -- applying a function within a context which produces a new context

(>>=) :: Monad       m =>   m a -> (a -> m b) -> m b

With this we can shorten countReader to

countReader = count >>> arrM (\x -> (\e -> pure (x * e)) =<< ask)
countReader = count >>> arrM (\x -> fmap (x * ) ask)
countReader = count >>> arrM (\x -> (x * ) <$> ask)

Instead of (Reader Int) we can use an arbitrarly complex data type for our config like.

data Config = Config
  { velocity    :: Int
  , soundVolume :: Int
  , isWindowed  :: Bool
  -- ...
  }

and then use asks velocity instead of ask.

ReaderT

[FrpRefac16] 4. : Monads and monad transfomers have associated execution functions to run computations and extract results, consuming or trapping effects in less structured environments. For instance, in the monad stack ReaderT e m we can eliminate the layer ReaderT e with runReaderT r :: e -> ReaderT e m a -> m a, obtaining a value in the monad m.

If we use a ReaderT now, like it’s used in the paper, you have to remember that it still a Monad and the MSF needs another Monad type.

countReaderT :: Monad m => MSF (ReaderT Int m) () Int -- what is m going to be?
countReaderT = count >>> arrM (\x -> (x * ) <$> ask)

This is important because if we run it in main :: IO () it will infer the Monad type IO into the transformer.

Todo

? why does that matter? m is a free variable, so we cannot use it for anything specific. we might as well set it to Identity? but I’m getting “Couldn’t match expected type: IO t0 with actual type: Identity [Int]”

main :: IO ()
main = do
  ls <- runReaderT (embed countReaderT [(), (), ()]) 5
  print ls

-- countReaderT :: MSF (ReaderT Int IO) () Int

[FrpRefac16] 4.1: This execution method, however, is outside the invocation of embed, so we cannot make the game settings vary during runtime. To keep the ReaderT layer local to an MSF, we define a temporal execution function analogous to runReaderT (implemented using an unwrapping mechanism presented in Section 5).

WIWINWLH - Monad Transformers: It’s useful to remember that transformers compose outside-in but are unrolled inside out.

import Control.Monad.Trans.MSF.Reader -- note the MSF here, it is not: import Control.Monad.Trans.Reader

main = do
  embed (runReaderS_ countReaderT 3 &&& runReaderS_ countReaderT 5) [(), (), ()]
-- > [(3,5),(6,10),(9,15)]

(If you are confused of were the tuple comes from it’s the &&& parallel arrow combinator.)

ReaderT in paper

Warning

there is another error in the paper. we are actually using runReaderS_ here

From paper:

runReaderS  :: Monad m => MSF (ReaderT r m) a b -> r -> MSF m a b
runReaderS_ :: Monad m => MSF (ReaderT r m) a b -> MSF m (r,a) b
runReaderS_ :: Monad m => MSF (ReaderT s m) (s, a) b -> MSF m a b

From source:

runReaderS  :: Monad m => MSF (ReaderT r m) a b -> MSF m (r, a) b
runReaderS_ :: Monad m => MSF (ReaderT s m) a b -> s -> MSF m a b
readerS     :: Monad m => MSF m (r, a) b -> MSF (ReaderT r m) a b

import Control.Monad.Trans.MSF.Reader
import Data.MonadicStreamFunction

type Game = Ball
type Ball = Int

data GameSettings = GameSettings
  { leftPlayerPos  :: Int
  , rightPlayerPos :: Int
  }

type GameEnv m = ReaderT GameSettings m

ballToRight :: Monad m => MSF (GameEnv m) () Ball
ballToRight = count >>> arrM (\n -> (n+) <$> asks leftPlayerPos)

hitRight :: Monad m => MSF (GameEnv m) Ball Bool
hitRight = arrM $ \i -> (i >=) <$> asks rightPlayerPos

testMSF = ballToRight >>> (arr id &&& hitRight)

main :: IO [((Ball, Bool), (Ball, Bool))]
main = do
  embed (runReaderS_ testMSF (GameSettings 0 3)) (replicate 5 ())
  -- > [(1,False),(2,False),(3,True),(4,True),(5,True)]
  embed (runReaderS_ testMSF (GameSettings 0 2)) (replicate 5 ())
  -- > [(1,False),(2,True),(3,True),(4,True),(5,True)]
  embed (runReaderS_ testMSF (GameSettings 0 3) &&& runReaderS_ testMSF (GameSettings 0 2)) (replicate 5 ())
  -- > [((1,False),(1,False)),((2,False),(2,True)),((3,True),(3,True)),((4,True),(4,True)),((5,True),(5,True))]

readert.hs

>>> cabal repl readert
>>> main

WriterT

countReaderT :: Monad m => MSF (ReaderT Int (WriterT String m)) () Int
countReaderT = count >>>
  arrM (\x -> ask >>= (\e -> pure (x * e))) >>>
  arrM (\cv -> lift $ tell (show cv) >> pure cv)

main = do
  embed (runWriterS (runReaderS_ countReaderT 3)) [(), (), ()]

WriterT in paper

From paper:

runWriterS :: Monad m => MSF (WriterT r m) a b -> MSF m a (b, r)

From source:

runWriterS :: Monad m => MSF (WriterT r m) a b -> MSF m a (r, b)

type GameEnv m = WriterT [String] (ReaderT GameSettings m) -- the other way around? otherwise we would have to lift all existing code

ballToRight :: Monad m => MSF (GameEnv m) () Ball
ballToRight =
  count >>> liftS addLeftPlayerPos >>> liftS checkHitR -- liftS = arrM, addLeftPlayerPos is not defined (use lambda from previous section)
  where
    checkHitR :: n -> GameEnv m Int -- what is type n ?
    checkHitR n = do
      rp <- asks rightPlayerPos
      lift $ when (rp > n) $ tell ["Ball at " ++ show n] -- lift was missing?
      pure n -- need to return type Int
-- Couldn't match expected type ‘Int’ with actual type ‘n’. ‘n’ is a rigid type variable bound by

import Control.Monad
import Control.Monad.Trans
import Control.Monad.Trans.MSF.Reader
import Control.Monad.Trans.MSF.Writer
import FRP.BearRiver

type Game = Ball
type Ball = Int

data GameSettings = GameSettings
  { leftPlayerPos  :: Int
  , rightPlayerPos :: Int
  }

--type GameEnv m = ReaderT GameSettings m
--type GameEnv m = WriterT [String] (ReaderT GameSettings m)
type GameEnv m = ReaderT GameSettings (WriterT [String] m)

ballToRight :: Monad m => MSF (GameEnv m) () Ball
ballToRight = count >>> arrM (\n -> (n+) <$> asks leftPlayerPos) >>> arrM checkHitR
--ballToRight = count >>> arrM (\n -> (n+) <$> asks leftPlayerPos) >>> withSideEffect checkHitR
  where
    checkHitR :: Monad m => Int -> GameEnv m Int -- change Int to () when using withSideEffect
    checkHitR n = do
      rp <- asks rightPlayerPos
      lift $ when (rp > n) $ tell ["Ball at " ++ show n]
      pure n -- remove when using withSideEffect

hitRight :: Monad m => MSF (GameEnv m) Ball Bool
hitRight = arrM $ \i -> (i >=) <$> asks rightPlayerPos

testMSF = ballToRight >>> (arr id &&& hitRight)

main = do
  embed (runWriterS (runReaderS_ testMSF (GameSettings 0 3))) (replicate 5 ())

writert.hs

>>> cabal repl writert
>>> main

Other stuff

Todo

use mtl MonadReader variant on reader and writer examples

>>> cabal repl
>>> :m Control.Arrow Control.Monad.Identity Control.Monad.Trans.MSF.Reader Data.MonadicStreamFunction.InternalCore FRP.BearRiver
>>> :t unMSF
-- unMSF :: MSF m a b -> a -> m (b, MSF m a b)
>>> runIdentity (runReaderT (unMSF (constant 1.0) ()) 0.1)
-- error: No instance for (Show (MSF (ClockInfo Identity) () Double)) arising from a use of ‘print’
>>> let res = runIdentity (runReaderT (unMSF (constant 1.0) ()) 0.1)
>>> fst res
-- 1.0

>>> :m Control.Arrow Control.Monad.Identity Control.Monad.Trans.MSF.Reader Data.MonadicStreamFunction.InternalCore FRP.BearRiver
>>> :l src/Main
>>> :set -fbreak-on-error
>>> :trace fst $ runIdentity (runReaderT (unMSF (spring2 1.0 30.0 20.0) ()) 0.1)

Todo

incorporate Dunai Issue 245 - using embed with a constant 1.0 MSF to get (printable) results with an example for Yampa

main = do
  embed (count >>> arrM print) [(), (), ()]
-- > 1
-- > 2
-- > 3
-- > [(), (), ()]

If you only care for the side effects and want to ignore the returned list.

import Control.Monad.Trans.MSF.Maybe

main = do
  embed_ (count >>> arrM print) [(), (), ()]
-- > 1
-- > 2
-- > 3